Pattern

Trees

Traverse and manipulate hierarchical data structures.

8 Problems

0 Easy

8 Medium

0 Hard

How Trees Works

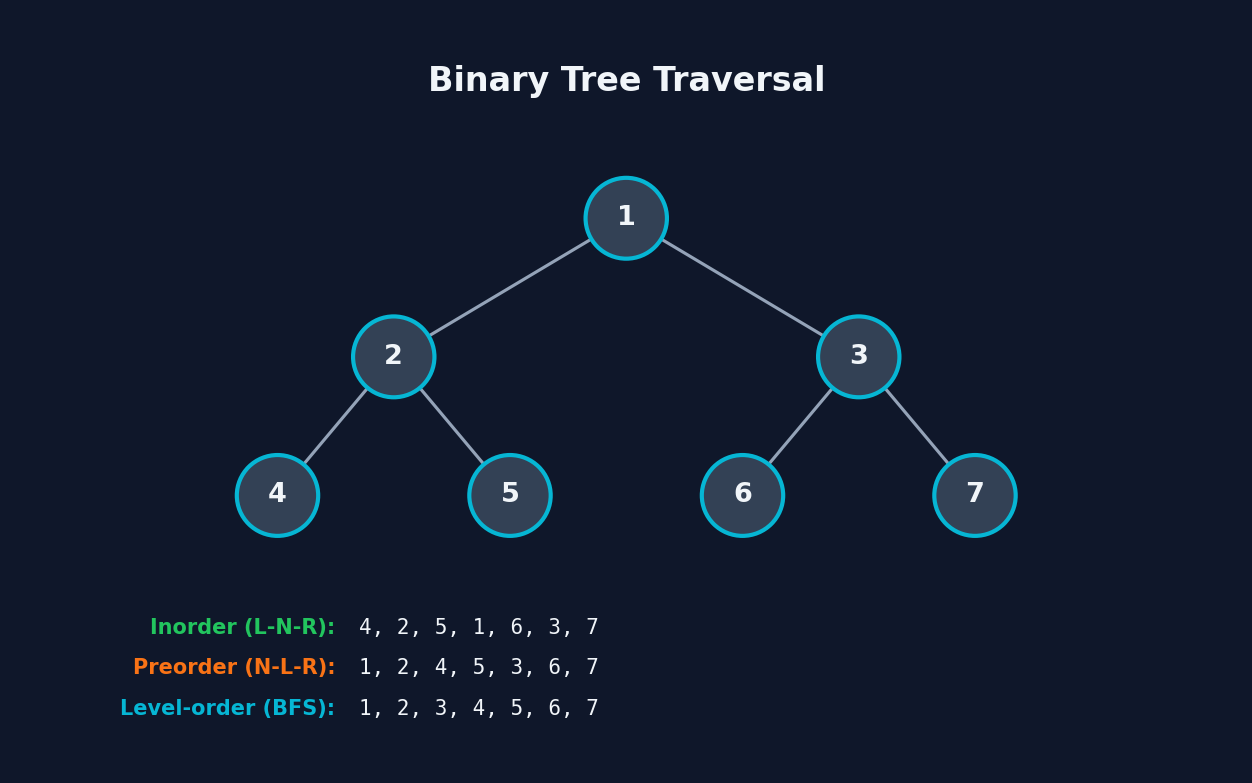
Tree problems are solved recursively by breaking them into subproblems at each node. At every node you have three choices: process the node before its children (preorder), between children (inorder), or after children (postorder). Most tree problems follow a pattern: define what information you need from left and right subtrees, combine it at the current node, and return the result upward. BFS (level-order) uses a queue to process nodes level by level, useful for shortest path or level-specific operations.

When to Use Trees

Pattern Recognition

Look for these trigger words in problem statements:

invert binary tree trees maximum depth of binary tree validate binary search tree lowest common ancestor of a binary search tree binary tree level order traversal binary tree right side view serialize and deserialize binary tree binary tree maximum path sum

Common Mistakes

Not handling the null/None base case (every recursive tree function needs it)
Confusing when to use DFS vs BFS — use DFS for path problems, BFS for level problems
Returning values incorrectly in recursive calls (the return value must propagate up)
Not considering that a tree might be unbalanced, leading to O(n) height instead of O(log n)

When NOT to Use Trees

When the structure has cycles (it's a graph, not a tree — use graph algorithms)
When you need to process all pairs of nodes (the recursive approach won't help)
When the problem is about sequences or arrays with no hierarchical structure

Practice Problems

Easy (0) Medium (8) Hard (0)

Invert Binary Tree medium Maximum Depth of Binary Tree medium Validate Binary Search Tree medium Lowest Common Ancestor of a Binary Search Tree medium Binary Tree Level Order Traversal medium Binary Tree Right Side View medium Serialize and Deserialize Binary Tree medium Binary Tree Maximum Path Sum medium

Master Trees

Build pattern recognition with interactive MCQs. Understand why to use Trees, not just how.

Download LeetEye Free