Pattern

Advanced Graphs

Master complex graph algorithms like shortest paths and minimum spanning trees.

6 Problems

0 Easy

0 Medium

6 Hard

How Advanced Graphs Works

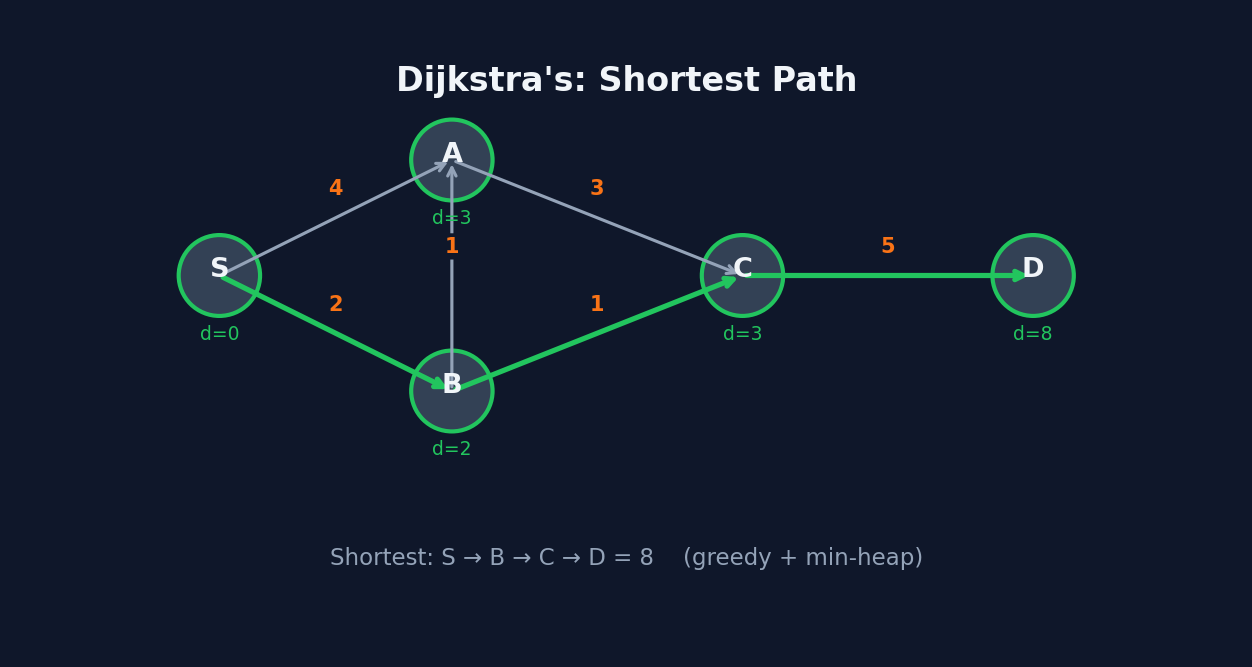
Advanced graph algorithms handle weighted edges, shortest paths, and minimum spanning trees. Dijkstra's algorithm finds shortest paths from a source using a priority queue, always expanding the closest unvisited node. Bellman-Ford handles negative weights by relaxing all edges V-1 times. Kruskal's and Prim's algorithms find minimum spanning trees. Topological sort orders nodes in a DAG so every edge goes from earlier to later, essential for dependency resolution.

When to Use Advanced Graphs

Pattern Recognition

Look for these trigger words in problem statements:

min cost to connect all points advanced-graphs network delay time swim in rising water alien dictionary cheapest flights within k stops reconstruct itinerary

Common Mistakes

Using Dijkstra with negative edge weights (it won't work — use Bellman-Ford)
Not using a priority queue for Dijkstra, resulting in O(V²) instead of O((V+E)log V)
Forgetting to detect negative cycles with Bellman-Ford
Applying topological sort to a graph with cycles (it only works on DAGs)

When NOT to Use Advanced Graphs

When all edges have equal weight (use simple BFS for shortest path)
When the graph is small enough for brute-force approaches
When the problem doesn't actually need shortest paths or spanning trees

Practice Problems

Easy (0) Medium (0) Hard (6)

Min Cost to Connect All Points hard Network Delay Time hard Swim in Rising Water hard Alien Dictionary hard Cheapest Flights Within K Stops hard Reconstruct Itinerary hard

Master Advanced Graphs

Build pattern recognition with interactive MCQs. Understand why to use Advanced Graphs, not just how.

Download LeetEye Free